The general problem: Data transmission over multipath channels

Differently from satellite communication where we have one single direct path from transmitter to receiver in the classical terrestrial broadcasting scenario we have to deal with a multipath- channel: The transmitted signal arrives at the receiver in various paths (see figure 0.1) of different length. Since multiple versions of the signal interfere with each other (inter symbol interference (ISI)) it becomes very hard to extract the original information.

 

  
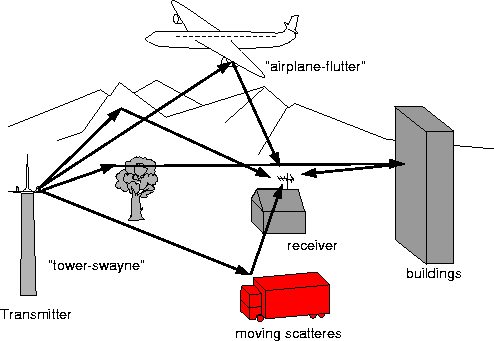
Figure 0.1: Multipath transmission in a broadcasting application

 

The common representation of the multipath channel is the channel impulse response (cir) of the channel which is the signal at the receiver if a single pulse is transmitted (figure 0.2).

 

  
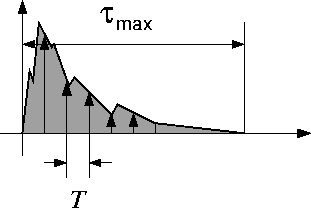
Figure 0.2: Effective length of cir

 

Let's assume a system transmitting discrete information in time intervals T. The critical measure concerning the multipath-channel is the delay 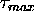of the longest path with respect to the earliest path. A received symbol can theoretically be influenced by 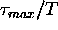previous symbols. This influence has to be estimated and compensated for in the receiver, a task which may become very challenging.

---

Single carrier approach

In figure 0.3 the general structure of a single carrier transmission system is depicted. The transmitted symbols are pulse formed by a transmitter filter. After passing the multipath channel in the receiver a filter matched to the channel is used to maximize signal to noise ratio a the device used to extract the data.

 

  
Figure 0.3: Basic structure of a single carrier system

 

The scenario we are dealing with in DVB-T is characterized by the following conditions:

• Transmission Rate:
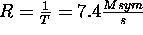
• Maximum channel delay:

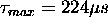
For the single carrier system this results in an ISI of:

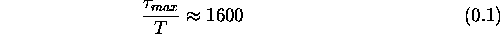
The complexity involved in removing this interference in the receiver is tremendous. In the scenario under consideration here, using such an approach will only lead to sub-optimal results. This is the main reason why the multi carrier approach presented in the next section has become so popular.

Multi carrier approach

 

Figure 0.4 shows the general structure of a multicarrier system.

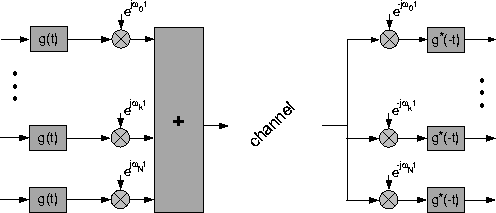
Figure 0.4: Basic structure of a multicarrier system

The original data stream of rate R is multiplexed into N parallel data streams of rate 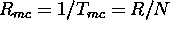each of the data streams is modulated with a different frequency and the resulting signals are transmitted together in the same band. Correspondingly the receiver consists of N parallel receiver paths. Due to the prolonged distance in between transmitted symbols the ISI for each sub system reduces to

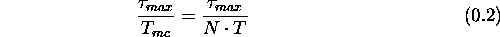
In the case of DVB-T we have N=8192 leading to an ISI of

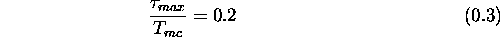
Such little ISI can often be tolerated and no extra counter measure such as an equalizer is needed. Alas as far as the complexity of a receiver is concerned a system with 8192 parallel paths still isn't feasible. This asks for a slight modification of the approach which leads us to the concept of OFDM.

Orthogonal Frequency Division Multiplexing

 

In OFDM the subcarrier pulse used for transmission is chosen to be rectangular. This has the advantage that the task of pulse forming and modulation can be performed by a simple Inverse Discrete Fourier Transform (IDFT) which can be implemented very efficiently as a I Fast Fourier Transform (IFFT). Accordingly in the receiver we only need a FFT to reverse this operation. According to the theorems of the Fourier Transform the rectangular pulse shape will lead to a sin(x)/x type of spectrum of the subcarriers (see figure 0.5).

  
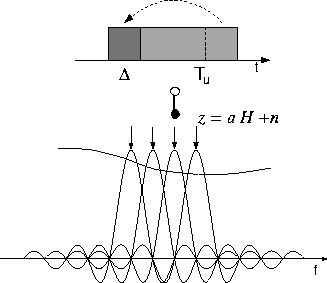
Figure 0.5: OFDM and the orthogonality principle

Obviously the spectrums of the subcarriers are not separated but overlap. The reason why the information transmitted over the carriers can still be separated is the so called orthogonality relation giving the method its name. By using an IFFT for modulation we implicitly chose the spacing of the subcarriers in such a way that at the frequency where we evaluate the received signal (indicated as arrows) all other signals are zero. In order for this orthogonality to be preserved the following must be true:

1. The receiver and the transmitter must be perfectly synchronized. This means they both must assume exactly the same modulation frequency and the same time-scale for transmission (which usually is not the case).
2. The analog components, part of transmitter and receiver, must be of very high quality.
3. There should be no multipath channel.

In particular the last point is quite a pity, since we have chosen this approach to combat the multipath channel. Fortunately there's an easy solution for this problem: The OFDM symbols are artificially prolonged by periodically repeating the 'tail' of the symbol and precede the symbol with it (see figure 0.5). At the receiver this so called guard interval is removed again. As long as the length of this interval 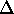is longer than the maximum channel delay 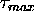all reflections of previous symbols are removed and the orthogonality is preserved. Of course this is not for free, since by preceding the useful part of length 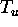by the guard interval we lose some parts of the signal that cannot be used for transmitting information. Taking all this into account the signal model for the OFDM transmission over a multipath channel becomes very simple: The transmitted symbols at time-slot l and subcarrier k are only disturbed by a factor 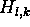which is the channel transfer function (the fourier transform of the cir) at the subcarrier frequency, an by additional white Gaussian noise n

 

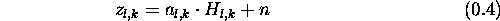
The influence of the channel can easily be removed dividing by .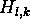

As far as the analog components are concerned experience has shown that in the broadcasting applications under consideration here, they are not so critical. What remains is to establish 'perfect' synchronization. This requires a very sophisticated receiver. The general structure and the receiver of such a receiver which we have developed for the DVB-T application, will be outlined in the next section.